Дуже часто при розв'язуванні задач, пов'язаних з обробкою масивів, необхідно
виконувати сортування його елементів за зростанням або спаданням. Такі задачі
мають велике практичне значення. Розглянемо деякі з методів, що дозволяють
впорядкувати елементи таблиць.
Всі існуючі методи сортування можна поділити
на три групи:
обмінні сортування - виконується обмін між собою двох деяких
(найчастіше сусідніх) елементів масивів, якщо відповідні елементи розташовані у
вихідному масиві невірно; процес повторюється або певну кількість разів, або
доки при черговому проході елементи в масиві не будуть переставлятися;
·
методи прямого вибору - в масиві вибирається елемент з певними властивостями
(наприклад, мінімум або максимум), а потім вибраний елемент становиться на своє
місце;
методи прямої вставки - послідовно вибирається елемент з масиву і
після визначення його місця у впорядкованому наборі даних вставляється
безпосередньо на своє місце.
Найбільш відомим обмінним сортуванням являється
метод "бульбашки". В ньому при послідовному проході по масиву
порівнюються два сусідніх елементи. Якщо їх розміщення являється неправильним
(наприклад, при впорядкуванні за зростанням лівий елемент більший за правий),
виконується взаємообмін елементів. Процес повторюється щонайменше N-1
разів, де N - кількість елементів в масиві.
Простіший алгоритм
"бульбашки" має наступний вигляд :
Program Bubble; {Сортування за зростанням}
Const N=20;
Var Mas:array[1..N] of integer;
i,j:integer; {i,j - змінні циклу}
Rez:integer; {Rez - додаткова змінна для
обміну елементів масиву між собою}
Begin
For i:=1 to N do
For j:=1 to N-1 do
If Mas[j]>Mas[j+1]
then
Begin
{Обмін елементів масиву через третю змінну}
Rez:=Mas[j];
Mas[j]:=Mas[j+1];
Mas[j+1]:=Rez;
End;
End.
Метод можна модифікувати, зменшуючи діапазон сортування після кожного
проходу, адже ясно, що після кожного проходу максимальний елемент масиву буде
"спливати наверх", тобто займати спочатку останню позицію таблиці, потім
передостанню і таке інше (дивись таблицю).
|
Початковий масив |
Прохід 1 |
Прохід 2 |
Прохід 3 |
Прохід 4 |
Прохід 5 |
Прохід 6 |
Прохід 7 |
Прохід 8 |
|
703
765
677
612
509
154
426
653
275
897
170
908
061
512
087
503 |
908
703
765
677
612
509
154
426
653
275
897
170
512
061
503
087 |
908
897
703
765
677
612
509
154
426
653
275
512
170
503
061
087 |
908
897
765
703
677
653
612
509
154
426
512
275
503
170
087
061 |
908
897
765
703
677
653
612
512
509
154
426
503
275
170
087
061 |
908
897
765
703
677
653
612
512
509
503
154
426
275
170
087
061 |
908
897
765
703
677
653
612
512
509
503
426
154
275
170
087
061 |
908
897
765
703
677
653
612
512
509
503
426
275
154
170
087
061 |
908
897
765
703
677
653
612
512
509
503
426
275
170
154
087
061 |
Програма, що реалізує описаний алгоритм має наступний вигляд:
Program Bubble; {Сортування за
зростанням} Const N=20; Var Mas:array[1..N]
of integer; i,j:integer; {i,j - змінні
циклу} Rez:integer; {Rez - додаткова змінна для
обміну елементів масиву між собою} Begin For i:=1
to N do For j:=1 to N-i do If
Mas[j]>Mas[j+1] then Begin {Обмін елементів
масиву через третю змінну} Rez:=Mas[j]; Mas[j]:=Mas[j+1];
Mas[j+1]:=Rez; End; End. Зверніть увагу, що в цьому алгоритмі у
вкладеному циклі, що безпосередньо здійснює порівняння елементів, змінна циклу
змінюється за іншим законом, ніж в попередньому випадку: від 1 до N-i, де
i - змінна циклу зовнішньої команди повторення.
Другий метод
модифікації алгоритму "бульбашки" полягає в тому, що ми вводимо додаткову змінну
булівського типу (так званий прапорець), яка буде фіксувати, при черговому
проході була здійснена хоча б одна перестановка елементів чи ні. Очевидно, що
якщо при черговому проході ні однієї перестановки не було зроблено, то масив вже
відсортований і процес перегляду можна припинити.
Домовимось вважати
прапорець "опущеним" (тобто рівним значенню false), якщо перестановки не
відбулося, і "піднятим" (рівним true) - в протилежному випадку. Крім
того, на забуваємо, що як і в попередньому випадку, після кожного проходу по
масиву найбільший елемент "спливає" наверх, тобто займає своє позицію. Тому
вводимо додаткову змінну k, що фіксує праву границю впорядкованості,
тобто при першому проході k=1 і ми впорядковуємо всі елементи від 1 до
N-1, на другому проході k=2 і будуть впорядковуватись всі елементи
від 1 до N-2 (останній елемент вже впорядкований) і так далі.
Програма, що виконує описаний вище алгоритм, має наступний вигляд:
Program Bubble; {Сортування за зростанням}
Const N=20;
Var Mas:array[1..N] of integer;
i,j,k:integer; {i,j - змінні циклу, k - змінна,
що фіксує праву границю
впорядкування}
Rez:integer; {Rez - додаткова змінна для
обміну елементів масиву між собою}
Flag:Boolean; {Flag - змінна, що фіксує,
відбулася перестановка чи ні}
Begin
k:=1;
Repeat
Flag:=false;
{Робимо припущення, що масив відсортований, а
потім перевіряємо, чи правильним було це
припущення, тобто чи немає серед елементів таких,
що неправильно розташовані, якщо такі елементи
будуть, то ми їх переставляємо і Flag присвоюємо
значення true}
For i:=1 to N-k do
Begin
If Mas[i]>Mas[i+1]
then
Begin
{Обмін елементів масиву через третю змінну}
Rez:=Mas[i];
Mas[i]:=Mas[i+1];
Mas[i+1]:=Rez;
Flag:=true;
End;
k:=k-1;
Until Flag = false;
End.
Мовою блок-схем алгоритм сортування "бульбашкою" має наступний вигляд
(третій із запропонованих):
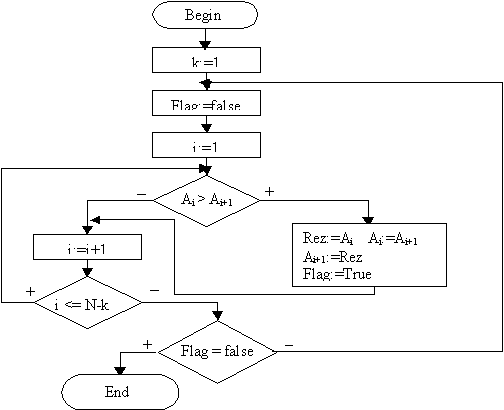
Другим методом сортування є метод прямого вибору. Один з його
різновидів полягає в тому, що вибирається мінімальний елемент масиву, а потім
виконується його обмін з першим елементом таблиці. Після цього перший елемент
вважається впорядкованим і процес повторюється для підмасиву, що містить на один
елемент менше за початковий, тобто елементи з 2-го до останнього. Процес
повторюється кожен раз для масиву, зменшеного на один елемент. Закінчується він
тоді, коли невпорядкований підмасив стає довжиною один елемент. Таким чином,
загальна кількість повторень дорівнює, як і в попередньому випадку, N-1
(N - кількість елементів масиву).
Програмна реалізація запропонованого
методу наведена нижче:
Program Selection;
Const N=20;
Var Mas:array[1..N] of integer;
i,j,Min,N_Min:integer;
Begin
For i:=1 to N-1 do
Begin
Min:=Mas[i]; {Зберігання еталону мінімуму}
N_Min:=i; {Зберігання номера мінімуму}
For j:=i+1 to N do
If Mas[j]then
Begin
Min:=Mas[j]; {Перевизначення еталону}
N_Min:=j; {Зберігання номеру еталону}
End;
{Обмін місцями мінімуму та першого елементу
підмасиву}
Mas[N_Min]:=Mas[i];
Mas[i]:=Min;
End;
End.
Зверніть увагу на те, що пошук мінімуму в програмі організований
стандартно, тобто перший елемент береться за еталон, а потім порівнюється з
усіма останніми
і, якщо новий елемент являється меншим за еталон, то
еталон переприсвоюється. Крім цього в алгоритмі запам'ятовується місце
знаходження цього мінімального елемента для того, щоб після виходу з циклу можна
було обміняти місцями знайдений мінімум і перший елемент підмасиву. Але так як
підмасив весь час змінює свій розмір, за еталон береться перший елемент саме
того підмасиву, який розглядається на наступному кроці, тобто
і-ий
елемент початкового масиву (
і - змінна зовнішнього циклу, що вказує на
початок нового підмасиву на кожному кроці).
Метод
прямої вставки
забезпечує вставку кожного елементу невпорядкованого масиву на своє
місце у вже впорядкований масив. На початку сортування масив розбивається на два
підмасиви, лівий з яких повинен бути впорядкованим, а правий - ні. У невідомому
масиві тільки один елемент можна вважати впорядкованим, тому спочатку ліва
відсортована частина складається всього з одного елементу. Потім по черзі
беруться елементи з другої невпорядкованої частини і для них знаходиться місце
вставки в першу частину таке, щоб впорядкованість не порушувалась. Це означає,
що при сортуванні за зростанням необхідно знайти таке місце в масиві, де лівий
елемент буде меншим або рівним за той, що вставляється, а правий - більшим за
той, що вставляється. Після цього в масиві необхідно зробити зсув елементів, щоб
звільнити місце, на яке і вставити черговий елемент.
Щоб оптимізувати
розглянутий алгоритм, можна поєднати зсув елементів з пошуком місця вставляння.
Для цього перевірки виконуються в зворотному напрямку від елемента, що потрібно
вставити до місця вставки Так як елемент, що вставляється, береться першим з
невпорядкованої частини масиву, то ліворуч від нього всі елементи вже
впорядковані. Тому фактично необхідно порівнювати даний елемент з усіма лівішими
від нього і, якщо даний елемент менший за той, з яким порівнюється, то
виконується обмін елементів. Елемент наче "пливе" ліворуч від свого початкового
місця розташування і процес цей припиняється, якщо знайдений елемент, не більший
за даний, або ми досягли початку масиву. Наприклад, даний такий масив:
12
-8 0 30 5 100 Розбиваємо його на дві частини. До першої входить єдиний
впорядкований елемент
{12}, а до другої - всі останні
{-8 0 30 5
100}. Запишемо тепер процес впорядкування по етапах:
І
етап: елемент, що впорядковується = -8.
1) -8 < 12, тому
виконується обмін, тобто після першого кроку масив має наступний вигляд:
-8
12 0 30 5 100
На цьому цикл припиняє свою роботу, тому що досягнуто початок
масиву (і=1).
ІІ етап: елемент, що впорядковується = 0.
1) 0
< 12, значить виконується обмін, тобто після першого кроку масив має
вигляд:
-8 0 12 30 5 100
2) 0 > -8 , значить обмін не виконується,
здійснюється вихід з циклу, масив залишається без змін.
ІІІ
етап: елемент, що впорядковується = 30.
1) 30 > 12, вхід до циклу
не відбувається, масив залишається без змін.
ІV етап: елемент,
що впорядковується = 5.
1) 5 < 30, виконується обмін, після перестановки
масив має вигляд:
-8 0 12 5 30 100
2) 5 < 12, здійснюється обмін, масив
набуває вигляду:
-8 0 5 12 30 100
3) 5 > 0, цикл припиняє свою роботу,
масив залишається без змін.
V етап: елемент, що впорядковується
= 100.
1) 100 > 30, вхід до циклу не відбувається, тому що умова відразу
хибна і масив залишається без змін.
Програму, що виконує запропонований
алгоритм, наведено далі:
Program Insert;
Const N=20;
Var Mas:array[1..N] of integer;
i,j,Rez:integer;
Begin
For i:=2 to N do
Begin
j:=i;
{Цикл працює доки, лівий елемент більший за
правий та не досягнуто початок масиву}
while (j>1) and (Mas[j]<Mas[j-1]) do
Begin
Rez:=Mas[j];
Mas[j]:=Mas[j-1];
Mas[j-1]:=Rez;
j:=j-1;
End;
End;
End.




