Задача №118.
Умова: Дано трикутник зі сторонами a,
b, c. Визначити, який це трикутник: гострокутний, тупокутний чи
прямокутний.
Для розв'язання цієї задачі необхідно нагадати дітям
наступне:
1) з відрізків заданої довжини можна утворити трикутник тільки в
тому випадку, якщо сума довжин будь-яких двох відрізків більше довжини третього
відрізка;
2) якщо з трьох відрізків можна побудувати трикутник, то він буде
прямокутним тоді й тільки тоді, коли виконується теорема Піфагора, тобто, коли
сума квадратів двох сторін дорівнює квадрату третьої (це співвідношення може
виконуватися для однієї пари сторін);
3) для гострокутного та тупокутного
трикутників теорема Піфагора перетворюється на нерівність, причому для
гострокутного повинні виконуватись всі три нерівності, а для тупокутного хоча б
одна (дійсно в гострокутному трикутникові всі кути менші за 90 градусів, а в
прямокутному та тупокутному хоча б один дорівнює або більше 90 градусів
відповідно).
Крім того, очевидно, що довжини всіх сторін не можуть бути
від'ємними або нульовими.
Отже, програма для розв'язання цієї задачі має
наступний вигляд:
Program Example_118;
Uses crt;
Var a,b,c:real;
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть довжини сторін: ’);
Readln(a,b,c);
If (a<=0) or (b<=0) or (c<=0)
Then writeln(‘Помилка вхідних даних.’)
Else
Begin
If (a+b < c) or (a+c < b) or (c+b < a)
Then writeln(‘З відрізків такої довжини утворити
трикутник неможливо.’)
Else
Begin
If (sqr(a)+sqr(b)=sqr(c)) or
(sqr(a)+sqr(c)=sqr(b)) or
(sqr(c)+sqr(b)=sqr(a))
then writeln(‘Трикутник прямокутний’);
If (sqr(a)+sqr(b) > sqr(c)) and
(sqr(a)+sqr(c) > sqr(b)) and
(sqr(c)+sqr(b) > sqr(a))
then writeln(‘Трикутник гострокутний’);
If (sqr(a)+sqr(b) < sqr(c)) or
(sqr(a)+sqr(c) < sqr(b)) or
(sqr(c)+sqr(b) < sqr(a))
then writeln(‘Трикутник тупокутний’);
end
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.
Задача №120(2).
Умова: Дано натуральне число N (N
<= 1000). Визначити суму першої і останньої цифр даного числа.
Для
розв'язання цієї задачі ми скористаємося стандартними операціями цілочисельного
ділення та остачі від ділення цілих чисел (операції div та
mod).
Нагадаємо, що результатом ділення числа націло на 10 буде ефект
"відкидання" молодшої цифри числа (відповідно при діленні на числа 100, 1000,
10000 тощо будемо "відкидати" дві, три або чотири цифри числа). Результатом ж
операції знаходження залишку від ділення на 10 буде остання цифра числа
(відповідно при знаходженні залишку від ділення на 100, 1000, 10000 будемо
отримувати дві останні, три останні, чотири останні цифри числа).
Наприклад:
234 div 10 = 23
9213 div 100 = 92
52
mod 10 = 2
2845 mod 1000 = 845.
Виходячи з усього сказаного,
програма буде мати наступний вигляд:
Program Example_120_2;
Uses crt;
Var N, First, Last : word; {N – дане число; First
– перша числа числа; Last –
остання цифра числа}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть число: ’);
Readln(N);
Last := N mod 10;
If (N>=0) and (N<10) then First:=0;
If (N>=10) and (N<100) then First:=N div 10;
If (N>=100) and (N<1000) then First:=N div 100;
If (N=1000) then First:=1;
Writeln(‘Сума першої та останньої цифр дорівнює ’,
First+Last);
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.
Задача №124.
Умова: Дано натуральне числа N (N
<= 99). Визначити, чи правильно, що N^2 дорівнює кубу суми цифр цього
числа.
Program Example_100_2;
Uses crt;
Var N, C1, C2 : word; {N – дане число; C1,C2 – перша
та друга цифри числа}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть число: ’);
Readln(N);
If N>99
Then writeln(‘Помилка вхідних даних’)
Else
Begin
C1:=N div 10;
C2:=N mod 10;
If sqr(N)=sqr(C1+C2)*(C1+C2)
Then writeln(‘Правильно.’)
Else Writeln(‘Не правильно.’);
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.
Задача №126(3).
Умова: Дано натуральне число N
(N <= 9999). Враховуючи всі чотири цифри числа, визначити, чи
правильно, що воно містить дві пари цифр, що повторюються.
Для розв'язання
цієї задачі теж користуємось операціями ділення націло та знаходження залишку
від ділення націло для виділення цифр числа, а потім розглядаємо всі можливі
варіанти співпадання пар цифр числа:
1) перша - друга та третя - четверта
цифри;
2) перша - третя та друга - четверта цифри;
3) перша - четверта та
друга - третя цифри.
Program Example_126_3;
Uses crt;
Var N,C1,C2,C3,C4:word; {N – дане число; C1,C2,C3,C4
– відповідні цифри числа}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть число: ’);
Readln(N);
If N>9999
Then writeln(‘Помилка вхідних даних’)
Else
Begin
C1:=N div 1000;
C2:=N div 100 mod 10;
C3:=N div 10 mod 10;
C4:=N mod 10;
If ((С1=С2) and (C3=C4)) or
((С1=С3) and (C2=C4)) or
((С1=С4) and (C2=C3))
Then writeln(‘Правильно.’)
Else Writeln(‘Не правильно.’);
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.
Задача №128(1).
Умова: Квадратний многочлен заданий
коефіцієнтами a, b, c, де а<>0. Визначити, чи
корені відповідного рівняння є парними числами.
Для розв'язання цієї задачі
необхідно нагадати дітям алгоритм знаходження коренів квадратного
рівняння:
1) обчислити дискримінант за формулою D = b^2 -
4ac;
2) якщо ми отримали від'ємне число, то коренів для розв'язку
квадратного рівняння з даними коефіцієнтами a, b, c не
існує;
3) якщо дискримінант не від'ємний, то корені рівняння знаходяться за
наступними співвідношеннями: 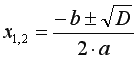
Парність коренів можна визначити, використовуючи операцію знаходження залишку
від цілочисельного ділення на 2 (парне число при цьому у залишку має 0, а
непарне - 1). Зверніть увагу тільки на те, що парність або непарність можна
визначити тільки для цілих чисел.
Program Example_128_1;
Uses crt;
Var a,b,c,D,X1,X2:real; {a,b,c – коефіцієнти
квадратного рівняння; D –
дискримінант; X1, X2 – корені
квадратного рівняння}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть коефіцієнти квадратного рівняння a,b,c: ’);
Readln(a,b,c);
If a=0
Then writeln(‘Помилка вхідних даних’)
Else
Begin
D:=sqr(b)-4*a*c;
If D<0
Then writeln(‘Рівняння не має розв”язків’)
Else
Begin
X1:=(-b-sqrt(D))/(2*a);
X2:=(-b+sqrt(D))/(2*a);
Writeln(‘Корені рівняння:’);
Writeln(‘X1=’,X1:8:2);
Writeln(‘X2=’,X2:8:2);
If (round(X1)<>X1)or(round(X2)<>X2)
Then writeln(‘Корені рівняння не являються
цілими числами.’)
else
if (round(X1) mod 2 =0) and
(round(X2) mod 2 =0)
then writeln(‘Корені рівняння парні’)
else writeln(‘Корені рівняння непарні’);
End;
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.
Задача №130.
Умова: Дано дійсні додатні числа a,
b, c, x, y. Визначити, чи пройде цеглина з ребрами
a, b, c у прямокутний отвір зі сторонами x та
y. Проштовхувати цеглину дозволяється лише так, щоб кожне з її ребер було
паралельним чи перпендикулярним кожній зі сторін отвору.
Для розв'язання цієї
задачі пропонується впорядкувати розміри отвору та розміри цеглини впорядкувати
за зростанням, тобто добитися того, щоб було a <= b <=
c та x <= y. Тоді перевірка зведеться до порівняння
розмірів отвору з найменшими розмірами цеглини (адже ми можемо цеглину
розвернути будь-яким боком, щоб проштовхнути її у отвір).
Program Example_130;
Uses crt;
Var a,b,c,x,y,S:real; {a,b,c – розміри цеглини; x,y –
розміри отвору, S – допоміжна
змінна для обміну місцями
значень двох змінних}
Begin
Clrscr; {Очищення екрану}
Write(‘Введіть розміри цеглини: ’);
Readln(a,b,c);
Write(‘Введіть розміри отвору: ‘);
Readln(x,y);
If (a<=0) or (b<-=0) or (c<=0) or (x<=0) or (y<=0)
Then writeln(‘Помилка вхідних даних.’)
Else
Begin
If a>b
Then
Begin
S:=a; a:=b; b:=S;
End;
If a>c
Then
Begin
S:=a; a:=c; c:=S;
End;
If b>c
Then
Begin
S:=b; b:=c; c:=S;
End;
If x>y
Then
Begin
S:=x; x:=y; y:=S;
End;
If (a<=x) and (b<=y)
Then writeln(‘Цеглина пройде у отвір.’)
else writeln(‘Цеглина не пройде у отвір.’)
End;
Readkey; {Затримка зображення на екрані до
натискання будь якої клавіші}
End.




