Задача №180.
Умова: Коли Василині Премудрій виповнилося 18
років, Чахлик Невмирущий вирішив взяти її заміж. Василина запитала Чохлика,
скільки у нього скринь із золотом. Чахлик сказав, що в нього зараз n
скринь і щороку додається ще по m скринь. Василина пообіцяла, що вийде
заміж тоді, коли у Чохлика буде k повних скринь із золотом. Скільки років
буде тоді нареченій?
Program Example_180;
Uses crt;
Var m,n,k:word; {n – початкова кількість скринь з
золотом, m – щорічний “прибуток”
Чахлика Невмирущого, k – “потреби”
Василини Премудрої}
Sum,Years:word; {Sum – щорічне накопичення Чахлика
Невмирущого, Years – вік Василини
Премудрої}
Begin
Clrscr;
Write(‘Введіть початкову кількість скринь з золотом: ’);
Readln(n);
Write(‘Введіть щорічний прибуток Чахлика: ’);
Readln(m);
Write(‘Введіть “потреби” Василини Премудрої: ’);
Readln(k);
Sum:=n; {Початковий “капітал” Чахлика}
Years:=18; {Початковий вік Василини}
While Sum<=k do
Begin
Sum:=Sum+m;
Years:=Years+1;
End;
Writeln(‘Василині вже виповнилося ’,Years,’ років.‘);
Readkey; {Затримка зображення на екрані}
End.
Задача №181.
Умова: Капосний папуга навчився висмикувати у
дідуся Василя волосся, яке ще залишилось у того на голові. Почавши з однієї
волосини, він щодня збільшував порцію вдвічі. Через скільки днів дідусеві не
знадобиться гребінець, якщо спочатку в нього на голові було аж N
волосин.
Program Example_181;
Uses crt;
Var N,Sum:word; {N – початкова кількість волосся у
дідуся Василя на голові, Sum –
щоденна кількість волосся на голові}
Day,K:word; {Day – кількість днів, протягом яких
папуга знущався над дідусем }
Begin
Clrscr;
Write(‘Введіть початкову кількість волосся на
голові у дідуся Василя: ’);
Readln(N);
Sum:=N;
Day:=0; {Початок знущання}
K:=1; {Початкова кількість вирваного
волосся}
While Sum>0 do
Begin
Sum:=Sum-K;
K:=2*K; {Кожен день кількість вирванного
волосся подвоювалась}
Day:=Day+1;
end;
writeln(‘У дідуся волосся закінчилося на ’,Day,’-й день.’);
Readkey; {Затримка зображення на екрані}
End.
Задача №197(2).
Умова: Дано натуральне число n.
Визначити суму цифр в числі.
Для розв'язку цієї задачі використаємо такий
штучний прийом: Щоб знайти суму цифр, ми повинні "брати" цифри по одній і
додавати їх одна до одної, а потім використану цифру "відкидати". На мові
Паскаль це нам дозволять зробити операції ділення націло та знаходження залишку
від цілочисельного ділення. Так, при діленні числа націло на 10 остання цифра
числа буде "відкидатися", а при знаходженні залишку від ділення націло ми
виділяємо останню цифру числа. Тобто:
123 div 10 = 12
3928 mod 10 =
8.
Процес буде повторюватись, доки від числа "нічого не залишиться", тобто,
доки воно не перетвориться на нуль. Програма, що реалізує описаний алгоритм має
наступний вигляд:
Program Example_197_2;
Uses crt;
Var n:longint; {N – дане число}
Sum:byte; {Sum – сума цифр числа}
Begin
Clrscr;
Sum:=0; {Сума цифр числа спочатку дорівнює 0}
Write(‘Введіть ціле число: ’);
Readln(N);
N:=abs(N);
While N>0 do
Begin
Sum:=Sum+N mod 10; {Знаходження суми цифр}
N:=N div 10; {“Відкидання” останньої
цифри числа }
End;
Writeln(‘Sum= ’,Sum);
Readkey; {Затримка зображення на екрані}
End.
Задача №200(2).
Умова: Дано дійсне число
а. Знайти таке найменше n, що 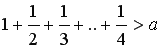 .
.
Очевидно, що
в даному випадку невідомо, на якому кроці ми досягнемо бажаного результату, тому
необхідно використати цикл з передумовою для перевірки досягнення бажаного
результату.
Зверніть увагу, що при деяких значеннях а дана сума ніколи
не досягне заданого значення. Наприклад, при від'ємному або дуже великому
значенні змінної а.
Program Example_200_2;
Uses crt;
Var n:word; {n – шукане число}
Rez,a:real; {Rez – результат обчислень, а –
граничне значення}
Begin
Clrscr;
n:=1; {Початкове значення n - 1}
Write(‘Введіть значення a: ’);
Readln(a);
Rez:=0; {Початкове значення суми}
While Rez<=a do
Begin
Rez:=Rez+1/n;
n:=n+1;
end;
Writeln(‘n= ’,n);
Readkey; {Затримка зображення на екрані}
End.
Задача №203(2). Умова: Знайти найбільше додатне
число n, для якого виконується умова: 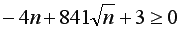 .
.
Очевидно,
що починаючи зі значення n=1 і збільшуючи його на одиницю після кожного
кроку, ми знайдемо таке ціле число, при якому вказана нерівність буде
вірною.
Program Example_203_2;
Uses crt;
Var n:word; {n – шукане число}
Begin
Clrscr;
n:=1;
While –4*n+841*sqrt(n)+3>=0 do n:=n+1;
Writeln(‘n= ’,n);
Readkey; {Затримка зображення на екрані}
End.
Задача №204.
Умова: Дано ціле число
m>1. Знайти найбільше число k, при якому виконується умова
4k < m.
Program Example_204;
Uses crt;
Var m,k,Rez:longint; {Rez – обчислення степеню 4}
Begin
Clrscr;
Write(‘Введіть значення m (m>1): ’);
Readln(m);
Rez:=1;
k:=0;
While Rezdo
Begin
k:=k+1;
Rez:=Rez*4;
End;
Writeln(‘k= ’,k);
Readkey; {Затримка зображення на екрані}
End.
Задача №208(1).
Умова: Під час обчислення результатів деяких
експериментів виникає необхідність отримання результату із заданою похибкою.
Нехай результатом є нескінченна сума, що задається певною формулою, і відома
похибка e (e > 0) для знаходження наближеного значення
результату. Будемо вважати, що необхідна точність досягнута, коли додавання
наступного доданку змінює суму на величину, меншу за e. Обчислити: 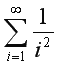
Program Example_208_1;
Uses crt;
Var i:word;
Rez,Epsilon:real; {Rez – результат обчислень,
Epsilon - похибка}
Begin
Clrscr;
Rez:=0; {Початкове значення дорівнює 0, тому
що результат являється накопиченням
суми}
Write(‘Введіть значення похибки (Е>0): ’);
Readln(Epsilon);
i:=1;
While 1/sqr(i)>Epsilon do
Begin
Rez:=Rez+1/sqr(i)
i:=i+1;
End;
Writeln(‘Rez= ’,Rez:8:2);
Readkey; {Затримка зображення на екрані}
End.
Задача №212.
Умова: Обчислити значення числа p,
використовуючи формулу 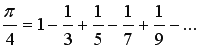
Визначити,
яка кількість доданків дає значення числа p з точністю до 3 знаків.
Для
організації циклу з передумовою в цій задачі необхідно мати еталон числа p для
порівняння з нескінченною сумою. Візьмемо в якості цього еталону значення
вбудованої функції Pi. Крім того, за умовою задачі нам необхідно отримати
результат з точністю до третьої цифри після коми. Пропоную для цього стандартне
число Pi і отриману нескінченну суму помножити на число 1000 та округлити
результат за допомогою функції round (отриману суму, крім того, необхідно
ще помножити на 4, так як сама сума являється чвертю числа p).
Зверніть увагу
також на те, що в нескінченній сумі доданки, що стоять на парних місцях
додаються зі знаком "+", а доданки на непарних місцях - віднімаються від суми.
Тобто в залежності від номера доданку (парний чи ні) ми організовуємо
знакочергування у нескінченній сумі. Результуюча програма для обчислення числа p
за допомогою нескінченної суми наведена нижче:
Program Example_212;
Uses crt;
Var i,n:word; {і – параметр циклу, n – кількість
доданків}
Rez_Pi:real; {Rez_Pi – обчислене значення числа
Pi}
Begin
Clrscr;
Rez_Pi:=0;
i:=1; {i – значення знаменника першого доданка}
n:=0; {n – доданків ще нема}
while round(pi*1000)=round(Rez_Pi*4000) do
Begin
If n mod 2 = 0
Then Rez_Pi:=Rez_Pi+1/i
Else Rez_Pi:=Rez_Pi-1/i;
i:=i+2;
n:=n+1;
End;
Writeln(‘Кількість необхідних доданків - ’,n);
Writeln(‘Порівняйте значення Pi: ’);
Writeln(‘Результат обчислень програми: ’,Rez_Pi:8:3);
Writeln(‘Вбудована функція: ’,Pi:8:3);
Readkey; {Затримка зображення на екрані}
End.




